矩阵加法

要使用卡尔曼滤波器方程，你需要学习矩阵加法。

例如，用于计算预测步骤之后的误差协方差矩阵的方程就需要矩阵加法：

$\mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}}$

或者，使用简单符号：

$\mathbf{P}' = \mathbf{F} \mathbf{P} \mathbf{F^T} + \mathbf{Q}$

矩阵加法通式

作为提示，下面是进行矩阵加法的通式：

$\mathbf{A} + \mathbf{B} = \begin{bmatrix}a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots &a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \ldots & a_{mn}\end{bmatrix} + \begin{bmatrix}b_{11} & b_{12} & \ldots & b_{1n}\\ b_{21} & b_{22} & \ldots &b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn}\end{bmatrix}$

$= \begin{bmatrix}a_{11}+b_{11} & a_{12}+b_{12} & \ldots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \ldots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \ldots & a_{mn}+b_{mn}\end{bmatrix}$

矩阵 A 中的第一个分量同矩阵 B 中的第一个分量相加。第二个分量同第二个分量相加，以此类推。

矩阵加法的具体例子

下面是矩阵加法的一个具体例子：

$\mathbf{A} + \mathbf{B} =\begin{bmatrix}17&25&6&2&16\\6&1&97&4&22\\80&8&54&15&65\\11&25&68&9&2\end{bmatrix}+\begin{bmatrix}3&14&1&7&42\\32&11&2&4&18\\19&81&4&8&5\\27&2&3&6&7\end{bmatrix} = \begin{bmatrix}20&39&7&9&58\\38&12&99&8&40\\99&89&58&23&70\\38&27&71&15&9\end{bmatrix}$

下图表示了如何计算总和。你将矩阵 A 中的一个分量同矩阵 B 中对应位置的分量相加。

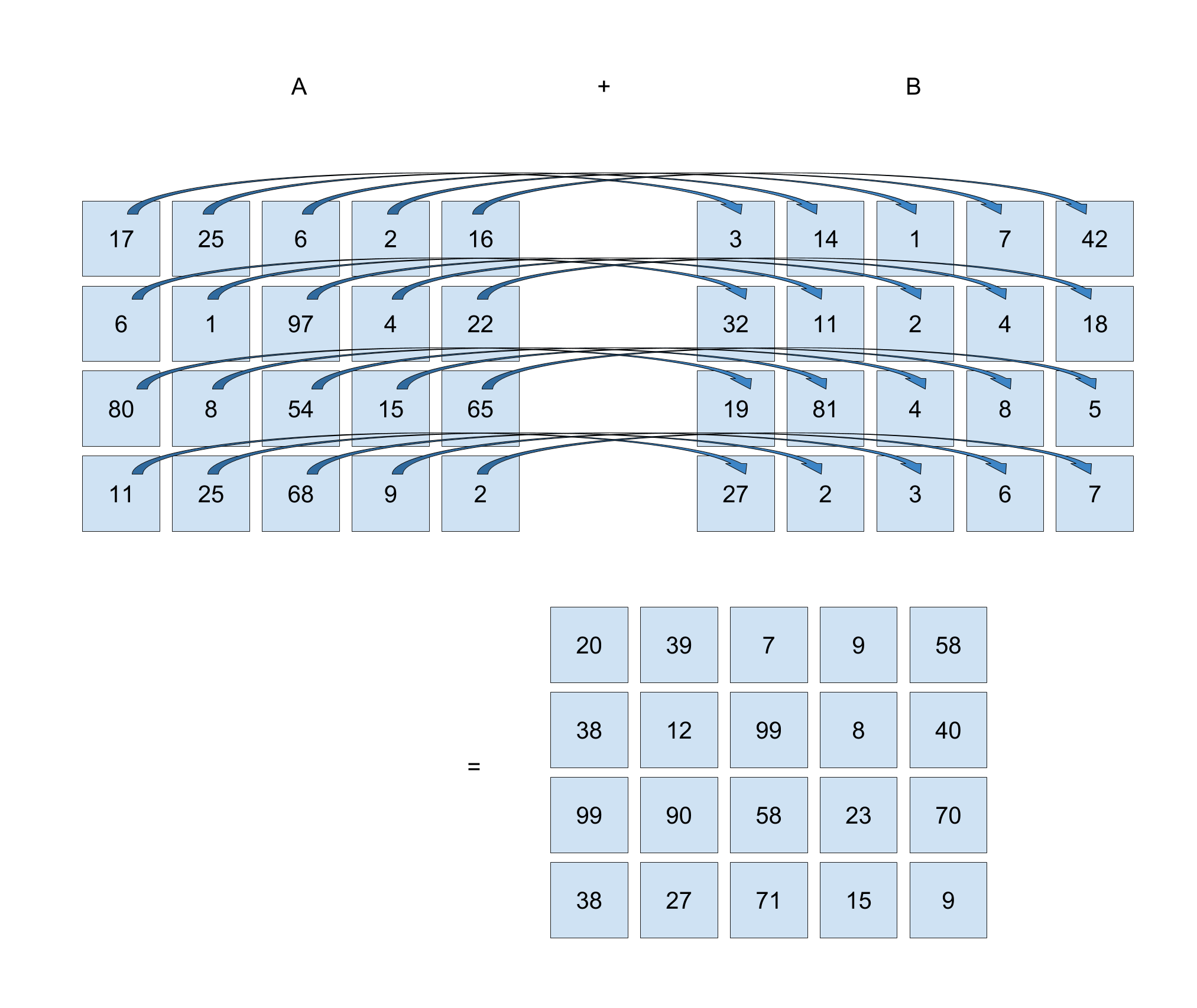
矩阵 A 中左上方的第一个分量为 17，矩阵 B 中左上方的第一个分量为 3。两者之和为 20，因此最终得到的矩阵中左上方的第一个分量为 20。

这里还有一个例子：矩阵 A 第二行第三列的分量为 97。矩阵 B 第二行第三列的分量为 2。两者之和为 99，因此最终得到的矩阵中第二行第三列的分量为99。

矩阵加法的特征

你会注意到，矩阵相加有一个重要特征：矩阵 A 和矩阵 B 的大小必须相同。换句话说，它们的行数和列数必须相同。我们回顾一下本页顶部的卡尔曼滤波器预测方程， $\mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}}$

这表示矩阵 $\mathbf{Q_{k}}$ 的大小必须等于 $\mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T}$ 相乘所得的矩阵大小。

此外，两个矩阵的总和大小也应该相同。因此， $\mathbf{P_{k|k-1}} \text{ 与 } \mathbf{Q_{k}}$ 的行数和列数也必须相同。

矩阵的减法

两个矩阵的减法也采用同样的方法计算。为了得到 $\mathbf{A} - \mathbf{B}$ ，你需要将矩阵 A 中的分量减去矩阵 B 中的对应分量。

编写矩阵加法

矩阵加法指对应位置的分量相加。因此对于 S = 矩阵 A + 矩阵 B，你需要这样操作：

S[0][0] = A[0][0] + B[0][0]
S[0][1] = A[0][1] + B[0][1]
S[0][2] = A[0][2] + B[0][2]
S[0][3] = A[0][3] + B[0][3]
.... etc

S[1][0] = A[1][0] + B[1][0]
S[1][1] = A[1][1] + B[1][1]
...etc.

然而，出于许多原因，这段代码并不十分高效。你需要为矩阵中的每一个分量编写一行代码。如果一个矩阵有 5 行 4 列，你需要编写 20 行代码。另一个问题是你并不能总是预先知道这个矩阵的尺寸有多大。你的代码也许需要容纳一个总和为 5x4 的矩阵。但接着你或许还需要计算一个 10x2 矩阵和其他数据配置的矩阵之和。

在这里，使用嵌套 for 循环语句再适合不过了。

使用 For 循环语句编写矩阵加法

在之前的练习中，你编写了代码来进行纯量乘法。你也编写了一个函数来输出矩阵。

矩阵加法的代码也非常相似。因此，试着在下一页的 IPython notebook 中自行练习。